
It's an exciting two-player strategy game that challenged you and an opponent to build a track with triangular playing pieces. The first player to complete the track or path of connected triangles between two arrows wins the game!
One player moves orange-track triangles; the other player moves yellow-track triangles. The one neutral white-track triangle can be moved by either player under certain circumstances.
Build a track by adding triangles to your own color-track and to your opponent's, too. It's how you angle the tangle of triangles that makes you a winner!

Components
- 1 plastic gameboard
- 3 rubber feet
- 15 plastic triangular pieces
- Instructions
Object of the Game
Be the first player to complete a track between two arrows.
Setup
Peel off the 3 rubber feet. Attach them to the bottom of the plastic gameboard unit. Just press them (sticky-side down) onto the 3 plastic legs.
Carefully break off individual playing pieces from their plastic supports. Players pick their playing pieces: one player moves the orange-track triangles; the other player moves the yellow-track triangles.
The neutral white-track triangle may be played by either challenger under certain circumstances.
Place the gameboard unit on a flat surface between you and your opponent.
Making Moves with the Color-track Triangles
There are 3 basic ways to position your playing pieces:
-
Place any one of your color triangles Into an empty space on the gameboard.
-
Or move one of your already positioned color triangles from one space on the gameboard to another space on the gameboard.
-
Or rotate one of your already positioned triangles in its present space to change the direction of the track.
Important: you may position your playing piece anywhere on the gameboard as long as It Is a legal move and as long as tho track does not lead off the gameboard.
Position your playing piece right next to an opponent's piece... or position it right next to one of your own pieces... or position It so it does not touch any other piece at all.
As the play progresses, several tracks may be built in various directions. The winner is the first player to complete a track of connected triangles between two arrows... If you position that last strategic triangle that completes the track, then you're the champion.

Game Play
-
Decide who plays first.
-
The Neutral Triangle: Player #1 must place the neutral white track triangle In one of the 6 center spaces on the gameboard. This Is Player #1's first legal move.
Hereafter the neutral triangle may be moved (from one space on the gameboard to another space on the gameboard) or rotated (revolved in Its present space on the gameboard to change the direction of the track) by either player EXCEPT under the following circumstances:
Exceptions to Neutral Triangle Move
-
If you move or rotate the neutral triangle, your opponent MAY NOT move or rotate the neutral triangle on his or her next turn.
-
If you moved or rotated the neutral triangle, you may move or rotate it again on your next turn. If you choose NOT to, your opponent Is then free to move or rotate the neutral triangle.
-
-
Player #2's first legal move Is to place one of his or her color triangles into an empty space on the gameboard. Remember, it can be placed anywhere... touching the neutral triangle... not touching the neutral triangle.
Just make sure its track does not lead off the gameboard (Rule 8. explains this off-the board position more clearly)!
-
Player #1's only legal second move is, either.
- Move or rotate the neutral triangle.
- Or place one of his or her color triangles Into an empty space on the gameboard. Just make sure Its track does not load off the board.
-
Play proceeds with players alternating turns and on each turn either placing, moving or rotating their own color triangles or moving and rotating tho neutral triangle when applicable (see exceptions to Neutral Triangle Movo under Rule 2., for further details).
-
You may never movo an opponent's color track trianglo.
-
You may never pass on your turn. . .you must either place, move or rotate a triangle.
-
Off-the Board, an illegal move: you may never place, move or rotate a triangle so that Its track points off the gameboard. To prevent this kind of move, the outside board spaces are built with small ribs to prevent the triangles from being positioned incorrectly and illegally.
Strategic Hint: you may make a defensive move by positioning one of your color track triangles to block off one of the two dark brown arrows (Note, you can only make this defensive move on the two dark brown arrows not on the two light brown arrows).
By doing this, you may rotate this cleverly positioned triangle at the crucial time to complete the track and win the game (See Figure 1, Triangle 1 for an example of this move).

End of the Game
The first player to complete the track between two arrows wins the game. See Figure 1. for an example of a winning track.
It Is possible that the game may end in a draw if players continue to make repetitive moves. If this happens, play on for a while, and If no one can complete the track, declare a draw!
The winning track is from arrow A to arrow B displayed by the dotted line! In this example, either player could have won.
The winner was the one who placed, moved or rotated his or her piece in such a way as to complete the track first.
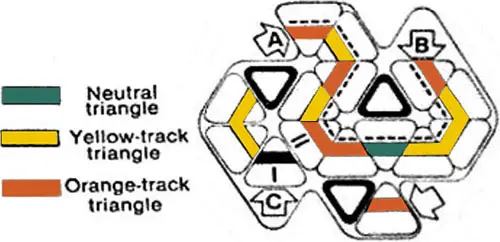 Figure1 |
Notice the orange-track player blocked off dark brown arrow C. with the triangle I.
By rotating triangles I and II on future moves, this player could have completed a winning track between arrows A and C. Unlorlunaloly, the winning track between arrows A and B was completed first!
Continue Reading

