Starving Artists is a time and resource management game for one to four players. Players compete to complete some of the world's most beautiful art in order to earn paint cubes, points and food.

Components

Starving Artists comes with everything you need to become a master paint-by-cube artist.

• 150 Paint Cubes
• 1 Paint Bag
• 8 Player Tokens
• 1 First Player Token
• Scoring Track.
• 92 Canvas Cards
• 4 Studio Cards

Canvas Cards

Squares: Canvases have a series of colored squares. These indicate which color paint cubes are required to complete the painting. Where a diamond shows more than one color, either color can be used.

Star value: 1 The total number of points the sold painting is worth.

Paint value: 2The maximum number of paint cubes you can collect for the sold painting.

Food value: 3 The amount of food you receive once sold.

Studio Cards

Each player will have one Studio Card which includes a nutrition track A, action track B, playerturn reference C, and paint palette D.

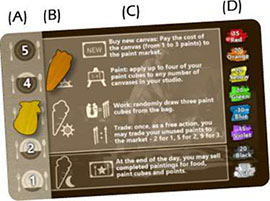
You can track your nutrition from one to five (full) using the nutrition track A and a player token along the left side.

When you're first player, track the days three phases using the action track B. First action phase during the morning, second during the day, and selling at night.

Object of the Game

You need to collect paint cubes and complete enough paintings to stay alive long enough to become the most famous paint-by-cube artist in the world.

Setup

If you're playing solo or you're interested in playing the Junior version rules, check the back of the rulebook for the changes to the setup.

1. Give the first player marker to the player who most recently visited a museum. Place it on the first action.

2. Give each player a matching set of player markers. Place one on the 0 of the scoring track and one on nutrition level 5 on the Studio Card.

3. Place all the paint cubes in the paint bag. Each player randomly draws six paint cubes from the bag and places them in their studio.

4. Shuffle the Canvas Cards and place them face down in the middle of the table.

5. To make the Canvas Market, turn over three Canvas Cards and place them in a line as follows:

During the game, you can purchase face-up Canvas Cards from the Canvas Market. The cost in paint cubes for a canvas is determined by its position in the Canvas Market from one paint cube (furthest from the deck) to three paint cubes.

When a canvas is purchased, cards are shifted down (toward one) and a new one is flipped over in the three slot.

Game Play

Starving Artists is played over a series of rounds representing days. Each day players take two actions (one in the morning and one in the afternoon ). At night, all players can sell their completed paintings.

At the start of each day

Add four paint cubes to the Paint Market. The first player randomly draws four paint cubes from the bag and put them in the center of the table into a Paint Market. You will add to it when you trade for paint cubes and buy canvases. You will take from it when you sell your completed paintings at the end of the day.

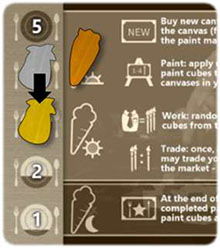
Lower your nutrition by one. Except for the first day, everyone lowers their nutrition by one on the nutrition track.

If your nutrition drops below one, return your paint cubes to the bag, you are out of the game. When this happens, the remaining players have one more day to complete their work before the game ends.

If the first player is eliminated, the first player marker passes immediately to the next surviving player.

Set the action to the morning. The first player places the first player marker on the first action of the day: morning.

The first player will move the carrot down the action track each time play returns to him or her.

Nutrition Tips

If you find yourself starving, a lot, try the following:

• Try to keep more than one canvas in your studio

• Try to avoid painting less than 3 cubes on an action

• Points aren't the only way to win

Actions

During each day, starting with the first player and going clockwise, you will take two actions, one at a time. In addition, once per day, you may take one of the free actions during one of your turns. You will "sell" completed paintings later.

On your turn, you can take any of the following actions:

Work: Randomly draw any three paint cubes from the paint bag and add them to your studio. You cannot paint with them yet.

Buy a new canvas: You may buy one canvas from the Canvas Market by paying the cost in paint cubes to the Paint Market. The cost is equal to its position in the Canvas Market.

Paint your canvas or canvases: You may apply up to four paint cubes from your studio to any number of canvases you own.

You do not need to paint all the squares you can, but you must apply a paint cube that matches the square's colors.

Painting Tips

You can apply your paint cubes to more than one canvas.

You can use either color paint cube on squares with two different colors.

The color palette at the bottom shows you the number (or range) of each color necessary to complete the painting.

Wild Cubes: You can use clear cubes as a substitute for any one square on a canvas. A canvas cannot have more than one wild cube.

Free Actions

In addition to your regular actions, once per day, you may do one of the following at any time during one of your turns (including before or after you take your action).

Trade for paint cubes: You may trade paint cubes from your studio for paint cubes in the Paint Market as follows:

• 2 paint cubes for 1 paint cube
• 5 paint cubes for 2 paint cubes
• 9 paint cubes for 3 paint cubes

You can use wild paint cubes (clear) from your studio to trade, but you cannot take them from the Paint Market.

Reset the Canvas Market: You can pay two paint cubes to the Paint Market to discard the current Canvas cards in the Canvas Market and turn over three new canvases placed in the order in which they're turned over.

You may immediately purchase any of the new canvases if you did not take your action.

Selling Completed Paintings

At the end of the day (night time), you may sell any number of your completed paintings for paint, points and food. As long as you won't starve, you do not have to sell your paintings and can wait until a later turn.

Announce

Starting with the first player and proceeding clockwise, players announce whether they intend to sell any paintings and indicate which paintings. Players cannot change their decision later.

Selling

If you are selling, then:

1. Raise your nutrition level by the Food Value on the painting. If you go over five nutrition, immediately take four paint cubes for each extra food.
2. Return all the paint cubes from your painting to the paint bag.
3. Advance you r scoring token around the track by the Star Value of the painting.

Getting Paid

Get Paid in Paint Cubes. Players are paid in paint cubes starting with the player with the highest Paint Value painting and proceeding in Paint Value order.

Players take turns taking paint cubes from the Paint Market up to the Paint Value of their painting or until the Paint Market is empty in a series of "collection actions". Players take the following amounts each collection action:

• Highest value painting: four paint cubes
• Second highest value: two paint cubes
• Everyone else: one paint cube.

During your collection actions, you may choose any of the paint cubes from the Paint Market. However, you can only take one wild paint cube per collection action.

Ties

If players' paintings have the same Paint Value, both players take the same number of paint cubes each collection action, but the order is determined by player order from the first player.

Selling more than one painting

If you sell more than one painting in a day, you treat each painting separately. You take paint cubes from the Paint Market for each painting separately, in separate collection actions.

End of the Day

After everyone has sold their paintings, the day ends. The first player marker is passed clockwise to the next player and a new day begins.

End of the Game

The game ends when:

• a player scores enough points
• a player completes enough paintings
• one day after a player starves

If no one starves, the Paint-by-Cube Master Painter is the first player to do either of the following (depending on player count):

• 2 players: complete 7 paintings or score 16 points
• 3 players: complete 6 paintings or score 14 points
• 4 players: complete 5 paintings or score 12 points

If someone does starve, and neither the painting nor point objectives were met, then the player with the highest point score wins. The winner could be the player who starved.

If both objectives are met by different players, the player with the most points win.

In the case of a tie based on points, the player with the most completed canvases wins. In case there is still a tie, the player who earned the most food wins. If there's still a tie, the player with the most unused paint cubes in their studio wins.

Optional Rules

Color Study

Instead of your free trade action during a day, you may place four paint cubes of the same color from your studio in the Paint Market and take any color cube of your choice from the bag. You can look.

Player Trades

Instead of your free trade action during a day, you may make a single offer to trade with all the players at the table. You must trade with the first player to accept your offer. You may not make another trade or offer to trade until the next day.

Last Supper

If you would otherwise starve at the start of the next turn (your nutrition is at one), you may discard one completed painting and raise your nutrition level by that painting's Star Value. The painting does not count as completed for end game purposes.

Colorblind Players

For players who are colorblind, or if you're in low light situations, you can use the following tips to help alleviate some issues.

Sort the cubes. As paint cubes are added to the Paint Market or drawn from the paint bag, identify them verbally and keep them in the same order as shown on the Studio and Canvas Cards: red, orange, yellow, green, blue, purple, black, and wild.

Use the color palette counts on the Canvas Cards. The squares aren't strictly necessary, just use the cube counts.

You can use the square count to know how many total paints are necessary to complete the painting.

Junior-player Rules

The following rules changes may help someone who's just learning to play games.

In general, play the game as described, but with the following changes:

• Start with one of each color in the Paint Market, except for the wild paint cubes.

• The cost of any canvas in the Canvas Market is one paint cube. Ignore the position of the canvases.

• When selling paintings, do not use the Paint Market. Draw the value of the painting from the paint bag.

• Use the Paint Market only to trade for paints. If there's more than four of a color in the market, return the extras to the paint bag.

Continue Reading