
Components

- 1 Game Board
- 1 Storage Bag
- 4 Tile Racks
- 78 Numerical Tiles
- 10 Blank Tiles
- 36 Equal (=) Tiles
- 9 Addition (+) Tiles
- 9 Subtraction (-) Tiles
- 9 Multiplication (x) Tiles
- 9 Division (÷) Tiles
- 24 Parentheses ( ) Tiles
- Instructions
Object of the Game
Be the player to score the most points by making true math statements (equations) to win.
Setup
Separate all of the tiles by carefully breaking them apart. Put the equal signs (=) and the clear parentheses ( ) to the side.
Remove all tiles with operations (such as division) that are not known by all players. Put all of the other tiles, including the blank tiles, into the storage bag.
Now, players draw 10 tiles from the storage bag and place them on their racks, without letting the other players see their tiles.

Game Play
The youngest player goes first. The first player places tiles on the board to form an equation, so that the first or last tile rests on the Start square on the center of the game board.
Players may pick up and use as many equal signs (=) or parentheses ( ) as they need.
Players may use as many equal signs (=) and parentheses ( ) as they need.
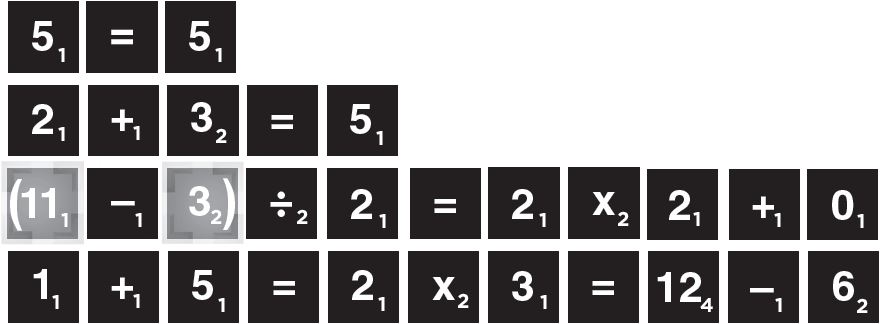
Note: Equations are read from left to right or from top to bottom. Each tile has a point value marked in the lower right corner of the tile.
On the board, there are special bonus squares that increase the value of the tile or of the entire equation.
The first player adds up the point values of the tiles used in his/her equation. If one or more tiles cover bonus squares, the score is increased as the squares dictate. Players replace tiles as needed from the bag so there are always 10 tiles on their racks.
The player to the left goes next. This player must make a new equation using one of the tiles from the first equation. This can be done in two ways: a new equation can be formed, or the first equation can be extended.

Note: The largest number on a tile is 12. Players may not place two tiles next to each other to make a larger number.
Tiles may not be moved after they are played, but parentheses can be put over a tile.

Instead of playing tiles, a player may skip a turn and exchange some or all of his/her tiles. The player places the tiles to be exchanged on the table, draws the same number of tiles from the bag, then puts the tiles on the table into the bag.
Types of Tiles
Parentheses: Players may use as many clear parentheses tiles as they wish. These tiles are placed over the number tiles to modify the order of operations or for multiplication.

Without parentheses, 2 + 3 - 1 + 4 would equal 8, not 0.

Parentheses can also be used for multiplication. In this way, the parentheses will help a player when there are no multiplication signs on his or her rack.
Blank Tiles: A blank tile may be used as any number or mathematical symbol. It remains the same number or symbol for the rest of the game.

Scoring
Point Value: Point values are found on the lower right corner of each tile. Blanks, equal signs, and parentheses have no point value.
A player adds the point values of all of the tiles used in the new equation. This includes the original tiles in an equation that has been made longer.
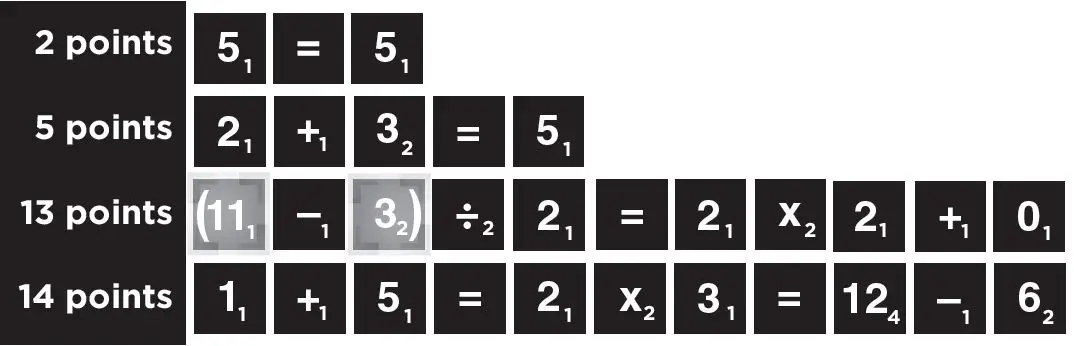
Bonus Squares: Bonus squares increase scores. They double or triple the point value of either one tile or the whole equation, but they can only be used one time.
For example, bonus squares that were already covered do not count when a player extends an equation. A player can use more than one bonus square on a turn.
When this happens, multiply the points for the playing piece square first, then multiply the points for the equation.
Scoring value of bonus squares on the game board:

10 Tile Bonus: A player who uses all 10 of the tiles on his or her rack in one turn gets 25 extra points.
End of the Game
The game ends when all of the tiles have been played, or when no other moves are possible.
Each player then subtracts the point values of the tiles on the rack from his/her total score. The player with the highest score wins!
Tips: Remember the Order of Operations!
Parentheses > Multiplication > Division > Addition > Subtraction
A calculator or math book may be used to challenge an equation. If the equation is untrue, the player takes back the tiles and loses that turn. Calculators should be used for challenges only.
Continue Reading


