Single Position
This is the easiest, first and most used technique to apply.
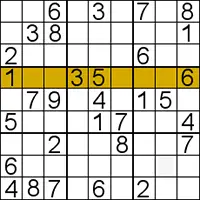
Choose a row, column or box, and then go through each of the numbers that hasn't already been placed.
Example: Look at the highlighted line and find single positions.
Where can you place a 8? Yes, at two columns, so we wait.
Where can you place a 7? Yes, at only one column, so we will place it.
Now, we can place the 8 in the remaining column.
Single Candidate

A very easy technique if you use pencilmarks to store candidates within each cell.
If you rule out all other possibilities for a particular cell, then the remaining candidate must fill the square.
If you find a cell, you can also elimanate all possibilities for this number in the row, column and block. And usually, you will have then also a single candidate left, etc...
Candidate Line

This technique don't tell you where exact to place a number, but it eliminates candidates (pencilmarks).
If you look within a box and see that all candidates of a particular number lie along a single line, then you can eliminate all candidates on that line outside the box.
So, even if you don't know exactly where to put the number yet, you can use this knowledge!

Double Pair
This technique relies on spotting two pairs of candidates for a value and using these to rule out candidates from other boxes.

Multi-Line
This is very similar to the Double Pairs technique, but is harder to see.
The candidates that occupy the lines can be spread across two of the blocks, and there can be several candidates in each line.
Naked Pairs and Triples

This clever technique is easier to use than to explain.
It works by seeing sets of pairs (triples) within an area (box, row, column).
They are called naked because whether they contain all of the set you're looking for or not, they won't be hidden underneath any other candidates.

Hidden Pairs and Triples
Hidden pairs and triples are quite a bit trickier to see.
(1-3) are hidden pairs because of a sneaking 2.
Continue Reading


